In my last post on the China Study II, I analyzed the effect of total and HDL cholesterol on mortality from all cardiovascular diseases. The main conclusion was that total and HDL cholesterol were protective. Total and HDL cholesterol usually increase with intake of animal foods, and particularly of animal fat. The lowest mortality from all cardiovascular diseases was in the highest total cholesterol range, 172.5 to 180; and the highest mortality in the lowest total cholesterol range, 120 to 127.5. The difference was quite large; the mortality in the lowest range was approximately 3.3 times higher than in the highest.
This post focuses on the intake of two main plant foods, namely wheat flour and rice intake, and their relationships with mortality from all cardiovascular diseases. After many exploratory multivariate analyses, wheat flour and rice emerged as the plant foods with the strongest associations with mortality from all cardiovascular diseases. Moreover, wheat flour and rice have a strong and inverse relationship with each other, which suggests a “consumption divide”. Since the data is from China in the late 1980s, it is likely that consumption of wheat flour is even higher now. As you’ll see, this picture is alarming.
The main model and results
All of the results reported here are from analyses conducted using WarpPLS. Below is the model with the main results of the analyses. (Click on it to enlarge. Use the "CRTL" and "+" keys to zoom in, and CRTL" and "-" to zoom out.) The arrows explore associations between variables, which are shown within ovals. The meaning of each variable is the following: SexM1F2 = sex, with 1 assigned to males and 2 to females; MVASC = mortality from all cardiovascular diseases (ages 35-69); TKCAL = total calorie intake per day; WHTFLOUR = wheat flour intake (g/day); and RICE = and rice intake (g/day).
The variables to the left of MVASC are the main predictors of interest in the model. The one to the right is a control variable – SexM1F2. The path coefficients (indicated as beta coefficients) reflect the strength of the relationships. A negative beta means that the relationship is negative; i.e., an increase in a variable is associated with a decrease in the variable that it points to. The P values indicate the statistical significance of the relationship; a P lower than 0.05 generally means a significant relationship (95 percent or higher likelihood that the relationship is “real”).
In summary, the model above seems to be telling us that:
- As rice intake increases, wheat flour intake decreases significantly (beta=-0.84; P<0.01). This relationship would be the same if the arrow pointed in the opposite direction. It suggests that there is a sharp divide between rice-consuming and wheat flour-consuming regions.
- As wheat flour intake increases, mortality from all cardiovascular diseases increases significantly (beta=0.32; P<0.01). This is after controlling for the effects of rice and total calorie intake. That is, wheat flour seems to have some inherent properties that make it bad for one’s health, even if one doesn’t consume that many calories.
- As rice intake increases, mortality from all cardiovascular diseases decreases significantly (beta=-0.24; P<0.01). This is after controlling for the effects of wheat flour and total calorie intake. That is, this effect is not entirely due to rice being consumed in place of wheat flour. Still, as you’ll see later in this post, this relationship is nonlinear. Excessive rice intake does not seem to be very good for one’s health either.
- Increases in wheat flour and rice intake are significantly associated with increases in total calorie intake (betas=0.25, 0.33; P<0.01). This may be due to wheat flour and rice intake: (a) being themselves, in terms of their own caloric content, main contributors to the total calorie intake; or (b) causing an increase in calorie intake from other sources. The former is more likely, given the effect below.
- The effect of total calorie intake on mortality from all cardiovascular diseases is insignificant when we control for the effects of rice and wheat flour intakes (beta=0.08; P=0.35). This suggests that neither wheat flour nor rice exerts an effect on mortality from all cardiovascular diseases by increasing total calorie intake from other food sources.
- Being female is significantly associated with a reduction in mortality from all cardiovascular diseases (beta=-0.24; P=0.01). This is to be expected. In other words, men are women with a few design flaws, so to speak. (This situation reverses itself a bit after menopause.)
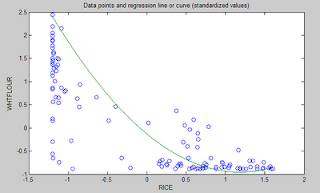
Wheat flour displaces rice
The graph below shows the shape of the association between wheat flour intake (WHTFLOUR) and rice intake (RICE). The values are provided in standardized format; e.g., 0 is the mean (a.k.a. average), 1 is one standard deviation above the mean, and so on. The curve is the best-fitting U curve obtained by the software. It actually has the shape of an exponential decay curve, which can be seen as a section of a U curve. This suggests that wheat flour consumption has strongly displaced rice consumption in several regions in China, and also that wherever rice consumption is high wheat flour consumption tends to be low.
As wheat flour intake goes up, so does cardiovascular disease mortality
The graphs below show the shapes of the association between wheat flour intake (WHTFLOUR) and mortality from all cardiovascular diseases (MVASC). In the first graph, the values are provided in standardized format; e.g., 0 is the mean (or average), 1 is one standard deviation above the mean, and so on. In the second graph, the values are provided in unstandardized format and organized in terciles (each of three equal intervals).
The curve in the first graph is the best-fitting U curve obtained by the software. It is a quasi-linear relationship. The higher the consumption of wheat flour in a county, the higher seems to be the mortality from all cardiovascular diseases. The second graph suggests that mortality in the third tercile, which represents a consumption of wheat flour of 501 to 751 g/day (a lot!), is 69 percent higher than mortality in the first tercile (0 to 251 g/day).
Rice seems to be protective, as long as intake is not too high
The graphs below show the shapes of the association between rice intake (RICE) and mortality from all cardiovascular diseases (MVASC). In the first graph, the values are provided in standardized format. In the second graph, the values are provided in unstandardized format and organized in terciles.
Here the relationship is more complex. The lowest mortality is clearly in the second tercile (206 to 412 g/day). There is a lot of variation in the first tercile, as suggested by the first graph with the U curve. (Remember, as rice intake goes down, wheat flour intake tends to go up.) The U curve here looks similar to the exponential decay curve shown earlier in the post, for the relationship between rice and wheat flour intake.
In fact, the shape of the association between rice intake and mortality from all cardiovascular diseases looks a bit like an “echo” of the shape of the relationship between rice and wheat flour intake. Here is what is creepy. This echo looks somewhat like the first curve (between rice and wheat flour intake), but with wheat flour intake replaced by “death” (i.e., mortality from all cardiovascular diseases).
What does this all mean?
- Wheat flour displacing rice does not look like a good thing. Wheat flour intake seems to have strongly displaced rice intake in the counties where it is heavily consumed. Generally speaking, that does not seem to have been a good thing. It looks like this is generally associated with increased mortality from all cardiovascular diseases.
- High glycemic index food consumption does not seem to be the problem here. Wheat flour and rice have very similar glycemic indices (but generally not glycemic loads; see below). Both lead to blood glucose and insulin spikes. Yet, rice consumption seems protective when it is not excessive. This is true in part (but not entirely) because it largely displaces wheat flour. Moreover, neither rice nor wheat flour consumption seems to be significantly associated with cardiovascular disease via an increase in total calorie consumption. This is a bit of a blow to the theory that high glycemic carbohydrates necessarily cause obesity, diabetes, and eventually cardiovascular disease.
- The problem with wheat flour is … hard to pinpoint, based on the results summarized here. Maybe it is the fact that it is an ultra-refined carbohydrate-rich food; less refined forms of wheat could be healthier. In fact, the glycemic loads of less refined carbohydrate-rich foods tend to be much lower than those of more refined ones. (Also, boiled brown rice has a glycemic load that is about three times lower than that of whole wheat bread; whereas the glycemic indices are about the same.) Maybe the problem is wheat flour's gluten content. Maybe it is a combination of various factors, including these.
Reference
Kock, N. (2010). WarpPLS 1.0 User Manual. Laredo, Texas: ScriptWarp Systems.
Acknowledgment and notes
- Many thanks are due to Dr. Campbell and his collaborators for collecting and compiling the data used in this analysis. The data is from this site, created by those researchers to disseminate their work in connection with a study often referred to as the “China Study II”. It has already been analyzed by other bloggers. Notable analyses have been conducted by Ricardo at Canibais e Reis, Stan at Heretic, and Denise at Raw Food SOS.
- The path coefficients (indicated as beta coefficients) reflect the strength of the relationships; they are a bit like standard univariate (or Pearson) correlation coefficients, except that they take into consideration multivariate relationships (they control for competing effects on each variable). Whenever nonlinear relationships were modeled, the path coefficients were automatically corrected by the software to account for nonlinearity.
- The software used here identifies non-cyclical and mono-cyclical relationships such as logarithmic, exponential, and hyperbolic decay relationships. Once a relationship is identified, data values are corrected and coefficients calculated. This is not the same as log-transforming data prior to analysis, which is widely used but only works if the underlying relationship is logarithmic. Otherwise, log-transforming data may distort the relationship even more than assuming that it is linear, which is what is done by most statistical software tools.
- The R-squared values reflect the percentage of explained variance for certain variables; the higher they are, the better the model fit with the data. In complex and multi-factorial phenomena such as health-related phenomena, many would consider an R-squared of 0.20 as acceptable. Still, such an R-squared would mean that 80 percent of the variance for a particularly variable is unexplained by the data.
- The P values have been calculated using a nonparametric technique, a form of resampling called jackknifing, which does not require the assumption that the data is normally distributed to be met. This and other related techniques also tend to yield more reliable results for small samples, and samples with outliers (as long as the outliers are “good” data, and are not the result of measurement error).
- Only two data points per county were used (for males and females). This increased the sample size of the dataset without artificially reducing variance, which is desirable since the dataset is relatively small. This also allowed for the test of commonsense assumptions (e.g., the protective effects of being female), which is always a good idea in a complex analysis because violation of commonsense assumptions may suggest data collection or analysis error. On the other hand, it required the inclusion of a sex variable as a control variable in the analysis, which is no big deal.
- Since all the data was collected around the same time (late 1980s), this analysis assumes a somewhat static pattern of consumption of rice and wheat flour. In other words, let us assume that variations in consumption of a particular food do lead to variations in mortality. Still, that effect will typically take years to manifest itself. This is a major limitation of this dataset and any related analyses.
- Mortality from schistosomiasis infection (MSCHIST) does not confound the results presented here. Only counties where no deaths from schistosomiasis infection were reported have been included in this analysis. Mortality from all cardiovascular diseases (MVASC) was measured using the variable M059 ALLVASCc (ages 35-69). See this post for other notes that apply here as well.
skip to main |
skip to sidebar
Recent Posts
Blogger Tricks
Blogger Themes
Text
Total Pageviews
Popular Posts
-
Moderate strength training has a number of health benefits, and is viewed by many as an important component of a natural lifestyle that appr...
-
This is one of those interesting studies where the authors start with some pre-conceived assumptions and end up concluding something else, s...
-
When protein-rich foods, like meat, are ingested they are first broken down into peptides through digestion. As digestion continues, peptide...
-
Adiponectin is a hormone exclusively secreted by body fat. This hormone has been recently gaining attention from researchers because of some...
-
Compensatory adaptation (CA) is an idea that is useful in the understanding of how the body reacts to inputs like dietary intake of macronu...
-
Below is a list of links to web sites that deal with health issues in general. I have moved them from the previous “favorite links” area to ...
-
The photos below, from Wikipedia, show two patterns of abdominal fat deposition. The one on the left is predominantly of subcutaneous abdomi...
-
My interview with Jimmy Moore should be up on the day that this post becomes available. (I usually write my posts on weekends and schedule ...
-
Several bacteria feed on lactose, the sugar found in milk, producing cheese for us as a byproduct of their feeding. This is why traditionall...
-
We all know that overweight along with obesity are for centuries no longer a fashion trend, instead it has even attracted many illnesses and...
Categories
- #trackmyphone
- 1000 bin challenge
- 1000 bins challenge
- 1000 photo challenge
- A guide to Zero Waste
- abdominal discomfort
- adiponectin
- adrenaline
- Aerosol recycling
- AGEs
- Akro professional catering products
- ALA
- albumin
- alcohol
- Aldeburgh Food Festival
- Almost Mrs Average
- Alpha Mummy
- alternative washing
- Amanda Holden
- amino acids
- anabolic steroids
- Anaerobic Digestion
- Ancestral Health Symposium
- Andrew Weil
- Animal Waste
- anorexia
- Apple Day
- arterial stiffness
- Asda refill trial
- Ask me about composting campaign
- atherosclerosis
- Atkins
- autophagy
- average faces
- Avoiding plastic bags
- Baglady
- barefoot running
- barefoot walking
- Bathroom waste
- BBC Radio Suffolk
- BBC Radio Suffolk Big Summer Declutter
- BBC Three Counties Radio
- BCAAs
- Beach Litter
- Becky John
- beef
- beef liver
- bell curve
- Berkeley Recycling
- BiBs
- Big Green Blog Gathering
- bile
- Biogas
- bipolar disorder
- birds
- bison
- Blenheim Films
- Blog Action Day
- Bloggers for Haiti
- Blogging
- Blogging Challenge
- blood acidity
- Blue Crane Recycling
- BMI
- body fat
- body fat loss
- boiling
- Bokashi
- Bokashi composting
- bone density
- book review
- Born to campaign
- Bottletop charity
- braces
- Brandon
- Brazilian sertão
- Brilliance in Blogging Awards
- Britain's Rubbish
- British Food Fortnight
- British Gas
- British Gas BritMums
- British grown flowers.
- British Mummy Bloggers
- Britmums
- Britmums Live
- Bury St Edmunds
- Bury St Edmunds Eco Fair
- Business Recycling
- butter
- Buy Nothing Day
- Buy Nothing New November
- Cabeza de Vaca
- cafestol
- calcium
- California
- calorie restriction
- Calories
- Cambridge City Council
- Cambridge Ecothrifter
- cancer
- cangaceiros
- Car Boot Sales
- carbohydrates
- cardiovascular disease
- carnivore
- Caroline Spelman
- catering waste
- causation without correlation
- cave painting
- Channel 4
- Charity Shops
- cheese
- Children
- Children's Parties
- China Study
- chlorogenic acid
- cholesterol
- Christmas
- Christmas 2009
- Christmas Leftovers
- Christmas List
- Christmas presents
- Christmas recycling
- Christmas selection boxes
- Christmas Tree
- chylomicron
- cirrhosis
- CIWM Awards for Environmental Excellence
- Clean Bin Project
- Cleaning
- Climate Change
- Climate Week 2012
- Clingfilm
- Co-operatives
- Coca-Cola
- coconut
- coffee
- cognition
- cold-induced thermogenesis
- Comedy Litte r Pick
- comfortable furniture
- Common Ground
- Community Groups
- Community repaint
- compensatory adaptation
- complexity
- Compost Awareness Week
- Compost Awareness Week 2012
- Composting
- Composting fruit peel
- Cooking
- Corona Save the Beach
- Coronation St Eco Refit
- Corporate gifts
- correlation does not imply causation
- cortisol
- costly traits
- Coventry
- cowboy coffee
- Crafty Christmas
- Creating the Greenest County
- Cumbria Flood Recovery Fund
- Cwm Harry
- Cybermummy 2011
- Daniel Suelo
- Darwin
- David Cameron
- Decluttering
- dental caries
- depression
- Designing out waste
- DHA
- diabetes
- dietary fat
- diseases of civilization
- Dispatches
- disposable cups
- Dobzhansky
- Documentary
- dog attack
- Don't be a tosser
- DoNation
- Dorset Cereal Little Blog Awards
- Dos Equis
- Dr. Jekyll and Mr. Hyde
- EACH Treehouse Appeal
- Eako
- East Devon Zero Waste Week
- Easter Packaging
- Eat Low Carbon
- eco-merchandise
- Ecoegg
- Ecoplastic
- ectomorph
- Edible Gardens
- Edinburgh Fringe Festival
- educatiing family about recycling
- egg
- El Cerrito
- Electric Vehicles
- Elvis and Kresse
- Emma Cooper
- Empowering Communities
- EMR
- endomorph
- endurance exercise
- endurance running
- Energy assessment
- Energy Conservation
- energy expenditure
- energyshare
- Enoughness
- EPA
- epigenetics
- Eric Pickles
- ethical lingerie
- Europe
- European Parliament
- European Week for Waste Reduction 2012
- Event Recycling
- evolution
- EWWR
- examples of reuse
- exercise injuries
- Fabmums
- Fabric Conditioner
- facial beauty
- Fake Plastic Fish
- familial hypercholesteromia
- Farmers Markets
- fasting
- fat loss
- fat-soluble vitamins
- FCC Environment
- Feeding the 5000
- Feeding5K
- Felixstowe
- Felixstroll
- filet mignon
- Fill your house for Free
- financial savings
- Fire-hose
- fish
- fish oil
- Fisher
- fit2fat2fit experiment
- five year phone challenge
- fixation
- flashbulb memories
- Flavour bombs
- food
- Food banks
- Food Donation Connection
- Food Waste
- Food Waste Bill 2012
- FoodCycle
- Footprint Friends
- Ford recycling
- Fran Crowe
- free fatty acid
- free running
- Freegle
- Friedewald LDL equation
- fructose
- fruit
- Furniture Re-use Network
- gallbladder
- Gardening
- gender
- genes
- genetics
- George Clarke
- ghrelin
- Give A Car
- Give and Take Day
- Give it for good
- Giving up rubbish for Lent
- Glamorous sheds
- Gleaning
- glucagon
- gluconeogenesis
- glucose
- glycation
- glycemic index
- glycemic load
- glycogen depletion
- glycogenesis
- grain-fed meat
- Grand Designs Live 2011
- Grand Designs Live 2012
- grass-fed meat
- Greatfun4kids
- Green Heroes
- Green Living Forum
- Green Paper
- Greg Rutherford
- ground meat
- Grow your own
- Growing vegetables
- Growing vegetables at school
- Grown in Britain Cookbook
- growth hormone
- Hadleigh HWRC
- haemochromatosis
- Haldane
- Hamilton
- Happy 101
- Hard Plastic
- Hard Plastic recycling
- HbA1c
- HCE
- HDL
- health management software
- heart disease
- Hen night novelties
- Henry and Jayne
- Hexam River Hydro
- Hexham River Hydro
- High Five Meme
- high-heat cooking
- Highlights
- Hilary Benn
- Holiday Season
- Holland and Barrett; Zero Waste; Reducing Packaging
- HOMA
- Home Composting
- Home insulation
- hormesis
- Hot yoga
- How do you squash yours
- How to reduce waste
- humor
- hunger
- hunter-gatherer
- hydrogenated fats
- hyperglycemia
- hypertension
- hypoglycemia
- immortality
- immunocompetence
- income
- Independent on Sunday
- industrial beverages
- infectious diseases
- inflammation
- information overload
- Inspire East
- Institution of Mechanical Engineers report 2013
- insulin
- intelligence
- interesting people
- interleukin-10
- interleukin-6
- intermittent fasting
- International Downshifting Week
- intima-media thickness
- Inuit
- iPhone
- Ipswich Borough
- Iranian LDL equation
- iron overload
- ischemia
- ITV1
- J curve
- jagunço
- James Hazell
- Jeremy Irons
- jerky
- Jessica Ennis
- jet lag
- Jimmy Moore
- Joanna Boardman
- John Naish
- John Stone experiment
- Jonathan Vernon-Smith
- Joy Blizzard
- Julie Day
- kahweol
- Karankawas
- Karen Cannard
- Karen Ford
- Keeping Chickens
- Kenco
- kerbside sorting
- Kerry McCarthy
- ketones
- ketosis
- Kevin McCloud
- Kevin's Green Heroes
- kidney stones
- Kids
- Kids' Challenge
- Kimura
- Kleiber's law
- Kwaśniewski
- Lamarckian inheritance
- LDL
- LEARN
- Leftovers
- Lent
- leptin
- Letsrecycle awards for excellence in waste and recycling
- links
- lipids
- lipotoxicity
- Litter problems
- liver disease
- Living ASAP
- local flowers
- local food
- local government
- London 2012
- London Zoo
- longevity
- Love Food Hate Waste
- low back pain
- low carb
- low T
- low testosterone
- Lp(a)
- magnesium
- Maillard reaction
- Making 2020 Zero Waste Work Conference
- Making Bath Bombs
- Mal Williams
- malocclusion
- Man Made Home
- manic-depressive disorder
- Marin Sanitary Services
- Mark and Spencer
- Mark Goodier
- markets
- Master Composters
- materials exchange
- Materials Recycling Facility (MRF)
- mating
- Mattress Recycling
- Maynard Smith
- Mayr
- MBA Polymers
- meatballs
- meatloaf
- meatza
- meditation
- Meet the bin slimmers
- Melissa Shoes
- mental health
- mercury
- mesomorph
- metabolic rate
- metabolic syndrome
- metformin
- methylglyoxal
- microwave oven
- Mid Suffolk
- Minamata disease
- Missing Midwives
- Mo Farah
- Mobile Phone Recycling
- Monday Meeting
- monounsaturated fat
- Moreton Hall
- mortality
- most interesting man
- Mothers Day
- Mothers for other mothers
- multivariate analysis
- Mumsnet
- muscle gain
- muscle loss
- Music Sales
- my experience
- My Zero Waste
- myopia
- myostatin
- myzerowaste.com
- National Baking Week
- National Weight Control Registry
- National Zero Waste Week 2009
- National Zero Waste Week 2010
- National Zero Waste Week 2011
- National Zero Waste Week 2012
- NEAT
- Nesta
- Nesta Waste Reduction Challenge
- Nestle
- New Year
- New year's resolutions
- Newlife Paints
- News Reports
- Newsy
- niacin
- nitrogen balance
- Nixdminx
- No child born to die
- No Impact Man
- noradrenaline
- Norfolk
- nutrition
- nuts
- O2Recycle
- obesity
- offal
- Okinawa
- Oliver Heath
- Oliver Ling
- Olympic Games Sustainability Challenge
- Olympics Zero Waste Protocol
- omega-3
- omega-6
- omega-6 to omega-3 ratio
- OPRL
- Optimal Diet
- Oregon Sudden Unexpected Death Study
- Ornamental melons
- Ornish
- osteopathy
- osteoporosis
- overfeeding
- Oxfam
- Packaging waste
- paleo diet
- palmitate
- palmitic acid
- pasteurization
- Paul Connett
- personality traits
- placebo effect
- Plains Indians
- planetshifter
- plaque
- Plastic Coathangers
- Plastic film recycling
- play
- Pledge ASAP
- Politics
- pollen allergies
- Polyprint
- pork
- potassium
- potassium to sodium ratio
- Poverty
- power napping
- Precycling
- presbyopia
- Presents Sense
- pressure-cooking
- Price
- primal workout
- Primary curriculum
- Prince Charles
- Procter and Gamble
- Professor Brian Cox
- promotional gift
- protein
- psychosomatic disorder
- Queens's market Newham
- R Factor
- Ramadan
- range of variation
- reactive hypoglycemia
- recent common ancestor
- recipe
- Recontextualising
- Recycle Now
- Recycle on the go
- Recycle Week
- Recycle Week 2010
- Recycle Week 2011
- Recycle Week 2012
- Recycled Cardboard Christmas Tree
- Recycled Christmas Carnival
- Recycled Clothes Show
- RecycleMobilePhones.co.uk
- Recycling
- Recycling at festivals
- Recycling bubblewrap
- Recycling Champion of the Year Finalist
- Recycling Champions
- Recycling Christmas Card
- recycling communications
- Recycling Electricals
- Recycling in Schools
- Recycling in Switzerland
- Recycling Innovations
- Recycling labels
- recycling on the go
- recycling paint
- Recycling pants
- Recycling plastic film
- recycling systems
- Recycling textiles
- Recyclometer
- red meat
- Reduced packaging
- Reducing carbon; wedding anniversary; 10:10
- Reducing Food Waste
- Reducing Packaging
- Reducing Waste
- ree Counties Radio
- refined carbs
- religion
- Renewable Idea
- repairing
- research
- resistance exercise
- resistant starch
- resistin
- Reusable cups
- Reuse
- Reuse Centres
- Reusing Christmas Cards
- reverse causation
- rice
- Richard Dimbleby Lecture
- rigid plastic recycling
- Ring Pull Project
- River Cottage
- Roasted Tomato Soup
- roasting
- Rob Dunger
- Robert Fulford
- Robert Llewellyn
- round steak
- Royce Gracie
- rPET
- Rubbish Diet Shropshire
- RWM with CIWM
- sainsbury's
- Sainsbury's Energy
- Saints Cafe
- Sale shopping
- San Francisco
- sardines
- satiety
- saturated fat
- Save the Children
- Saving energy
- schizophrenia
- Scouts
- seed oils
- self-experimentation
- sertanejo
- shampoo bottles
- Shedwyn
- Shirley Lewis
- Shopping with waste in mind
- Shrewsbury Transition Town
- shrimp
- Shropshire
- Shropshire Rubbish Diet
- Shwop Lab
- Shwopping
- simple living
- simplicity
- skin pigmentation
- skinny-fat
- sleep
- slow-cooking
- Smart Meters
- Smart Mums
- SmartMums
- smartphone
- smelts
- smoking
- Smoothies
- Soaper Heroes
- soccer
- Social Enterprise
- sodium
- South Korea
- spirituality
- Sponsorship
- St Edmundsbury
- St Edmundsbury Borough Council
- St Nicholas Hospice
- Stand up for recycling out on the streets
- standard deviation
- starch
- starvation
- statistics
- Straw Wars
- strength training
- stress
- Suburban Henkeeping
- sudden cardiac arrest
- Suffolk
- Suffolk Circle
- Suffolk County Council
- Suffolk Fire Service
- Suffolk Household Waste Recycling Centres
- Suffolk HWRCs
- Suffolk Recycling
- Suffolk Seven Streets
- Suffolk Show
- Suffolk:Creating the greenest county
- sugars
- Super Savvy Me
- supercompensation
- Supermarket recycling
- Supermarkets
- supernaturalism
- survival
- Sustainable Bury
- Sustainable Restaurant Association
- Swap Shop
- sweet potato
- Tags
- TEDxGreatPacificGarbagePatch
- Teenagers
- telomere
- tenderloin
- tentenuk
- testosterone
- Tetra Pak.
- Tetra Paks
- The Alternative Kitchen Garden
- The Baglady Productions
- The Big Tidy Up
- The Clean Bin Project
- The Coffee House
- The Eco Fair
- The Forgotten Feast
- The future of UK waste policy
- The Good Life
- The Green Thing
- The Ideal Home Show
- The Landfill Prize
- The Olympics
- The Rubbish Diet
- The Rubbish Diet Challenge
- The Rubbish Diet Challenge 2012
- The Rubbish Diet Challenge 2013
- The Suffolk Diet
- The War of the End of the World
- thermogenesis
- This is Rubbish
- Thornton's Budgens
- Thrifty Christmas
- Throwaway Britain
- Tips
- Tipton Litter Watch
- tired pancreas theory
- Tom Hunt
- TomsFeast
- Tonight
- Too Good to Waste
- tooth decay
- top sirloin
- Tracey Smith
- Trade Waste
- trans-fats
- Transition Shrewsbury
- Transition Towns
- Trashed Film
- travel
- triglyceride
- tripe
- Tristram Stuart
- Trivers
- tumor necrosis factor-alpha
- U curve
- UK Tour
- UKAware
- UKAware 2011
- unfiltered coffee
- Unusual challenges
- Unwanted presents
- Upcycling
- Urban Ore
- UVA
- UVB
- VAP test
- Vegetable steamers
- vegetarian
- Vehicle recycling
- viral diabetes
- visceral fat
- vitamin A
- vitamin C
- vitamin D
- vitamin E
- vitamin K2
- VLDL
- waist circumference
- waist-to-weight ratio
- Waitrose
- Wallace
- War of Canudos
- warppls
- Washington
- Waste
- Waste Plastics
- Waste Reduction
- Waste reduction challenge
- Waste Reduction Fortnight
- Waste Watch
- WEEE
- Weekly bin collections
- weight loss
- Weight Watchers
- Westminster Energy Environment and Transport Forum
- wheat
- white coat hypertension
- Who made your pants. ethical fashion
- Wiggly Wigglers
- Williams
- Wilson
- Wiltshire Wildlife Trust
- Wipe Out Waste awards
- Woman's Hour
- Women and Politics
- Worm cafe
- Wormery
- WOW Awards
- WRAP
- WRG
- Wright
- WWF
- www.myzerowaste.com
- Zahavi
- Zahavian traits
- Zambia
- Zero heroes
- Zero Waste
- Zero Waste Alliance UK
- Zero Waste Britain
- Zero Waste Campaigner
- Zero Waste Challenge
- Zero Waste Christmas
- Zero Waste Cleaning
- Zero Waste Communities
- Zero Waste Cosmetics
- Zero Waste documentary
- Zero Waste Europe
- Zero Waste Events
- Zero Waste Expert
- Zero waste flowers
- Zero Waste Gardening
- Zero Waste Home
- Zero Waste International Dialog 2013
- Zero Waste Places
- Zero Waste Shoes
- Zero Waste Standards
- Zero Waste UK Alliance
- Zero Waste Videos
- Zero Waste Week
- Zero Waste Week 2011
- Zero Waste Week 2013
- Zero Waste Week challenge
- Zone
- ZWIA
Archives
-
▼
2010
(170)
-
▼
September
(15)
- Income, obesity, and heart disease in US states
- Baglady's ASAP pledge programme
- Low nonexercise activity thermogenesis: Uncooperat...
- Strong causation can exist without any correlation...
- The China Study II: Wheat flour, rice, and cardiov...
- Can you help Blue Crane Recycling help people in n...
- Friday Fishcakes
- Sardine Surprise
- The China Study II: Cholesterol seems to protect a...
- Feel Good Chicken Soup at Saints Cafe
- The one that doesn't yet have a name
- Roasted tomato soup madam? Oh yes please.
- Low omega-6 to omega-3 ratio: Grain-fed meats or i...
- How to lose fat and gain muscle at the same time? ...
- Guess who'll be hanging out with Saints for Nation...
-
▼
September
(15)


 :.
:.

 1:30 PM
1:30 PM
 Unknown
Unknown






 Posted in:
Posted in: 







0 comments:
Post a Comment